Предлагаем для совместного решения и обсуждения еще несколько задач по Главе 6.
Задача 1.
Используя математическую индукцию, докажите, что
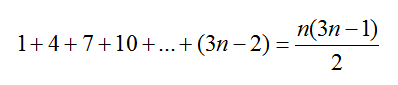
Предлагаем для совместного решения и обсуждения еще несколько задач по Главе 6.
Задача 1.
Используя математическую индукцию, докажите, что
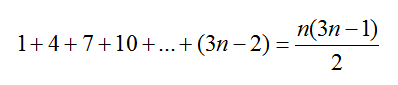
Задача 2
Используя математическую индукцию, докажите, что
Задача 3.
В компании из n человек (n > 3) каждый узнал по новой истории. За один телефонный разговор двое сообщают друг другу все известные им истории. Докажите, что за 2n – 4 разговоров все смогут узнать все новые истории.
Первую задачу решил достаточно просто и быстро. Для решения первой задачи предлагаю в качестве базиса индукции взять 1, тогда по формуле получаем ( 1 * ( 3 * 1 - 1) ) / 2 = 1, т.е. получили первый элемент последовательности, сделав индуктивный переход, n=2, получаем ( 2 * ( 3 * 2 - 1) ) / 2 =5, что соответствует сумме двух первых элементов последовательности.
Со второй возникли проблемы, в качестве базиса индукции я взял 2, по формуле получил (n + 1) / ( 2 * n ) = 3/4, произведение же двух дробей равно, ( 1 - 1/4) * (1 - 1/9 ) = 3/4 * 8/9 = 2/3, что не соответствует значению полученному по формуле.
Совершив индуктивный переход n=3 получил следующие данные, по формуле получаем, 4/6 или 2/3, Перемножив элементы получил следующие данные, 2/3 * ( 1 - 1/16 ) = 2/3 * 15/16 = 5/8. Из полученных данных я пришел к выводу, что формула не верна. Анализ решения навёл меня на мысль, что для нахождения произведения элементов последовательности следует использовать формулу ( n + 2 ) / ( 2 * n + 2).
По третьей задаче. ответить пока не готов, надо ещё раз её обдумать.
Для двойки рассмотрите 1 - 1/4 = 3/4, а не произведение, все получается.
Не думаю, что правильный подход, т.к. в таком случае, если для первого элемента взять номер два, это уже не очень корректно, но если взять для второго тройку, то есть совершить индуктивный переход, то мы опять таки придём к противоречию...
А нет, был не прав - нашел свою ошибку... беру свои слова обратно.
В первой задаче вы доказали только то, что утверждение верно при n=1 и n=2. Индуктивный переход - это доказательство того, что из P(n) следует P(n+1). Вы должны доказать это в общем виде, а не подставлять конкретные значения n. Если следовать вашей логике, я могу доказать, что все натуральные числа меньше 5. База: 1<5 - верно, индуктивный переход: n=2, 2<5 - опять верно. Значит, все натуральные числа меньше 5.
Вам нужно доказать, что из 1+4+...+(3n-2)=n(3n-1)/2 следуете, что 1+4+...+(3n-2)+(3(n+1)-2)=(n+1)(3(n+1)-1)/2.
Понял, спасибо!
Первые две задачки тривиальные, но набирать их проблематично. Поэтому я представлю своё решение только третьей задачи (она поинтересней).
Пусть n человек обмениваются всеми историями за k телефонных звонков. Допустим, к их компании добавляется n+1-й человек. Тогда, чтобы n+1 участников обменялись историями, пусть n+1-й человек позвонит 1-му человеку и сообщит свою историю. Затем за k телефонных разговоров первые n человек обмениваются историями, после чего каждый из первых n человек будет знать все n+1 истории. Чтобы их узнал n+1-й человек, пусть, допустим, 1-й ему позвонит и расскажет недостающие n-1 истории (одну историю n+1-й знает изначально, и одну ему рассказал 1-й при самом первом телефонном разговоре). Тогда при условии, что n человек обмениваются всеми историями за k телефонных звонков, n+1 человек делают это за k+2 звонка. Пусть f(n) – количество звонков, необходимых для n человек. Получаем рекуррентное соотношение:
f(n)=f(n-1)+2
Значит, задача сводится к нахождению решения этого соотношения в замкнутом виде. Но решение нам уже предоставили, значит, остаётся доказать, что это оно.
Итак, докажем, что f(n)=2n-4 (при n>3)
Индукция по n
База: n=4
1-й звонок: 1-й и 2-й обмениваются историями;
2-й звонок: 3-й и 4-й обмениваются историями;
3-й звонок: 1-й и 3-й обмениваются историями;
4-й звонок: 2-й и 4-й обмениваются историями.
За 4 звонка все участники узнали все истории.
f(4)=4=2*4-4 – верно
Индуктивный шаг: n=k
Пусть f(k)=2k-4, тогда
f(k+1)=f(k)+2=2k-4+2=2k+2-4=2(k+1)-4
Значит, f(n)=2n-4 (при n>3)
Ч. и т.д.
Замечательно! Класс!