Arnold Diffusion via Invariant Cylinders and Mather Variational Method
Курс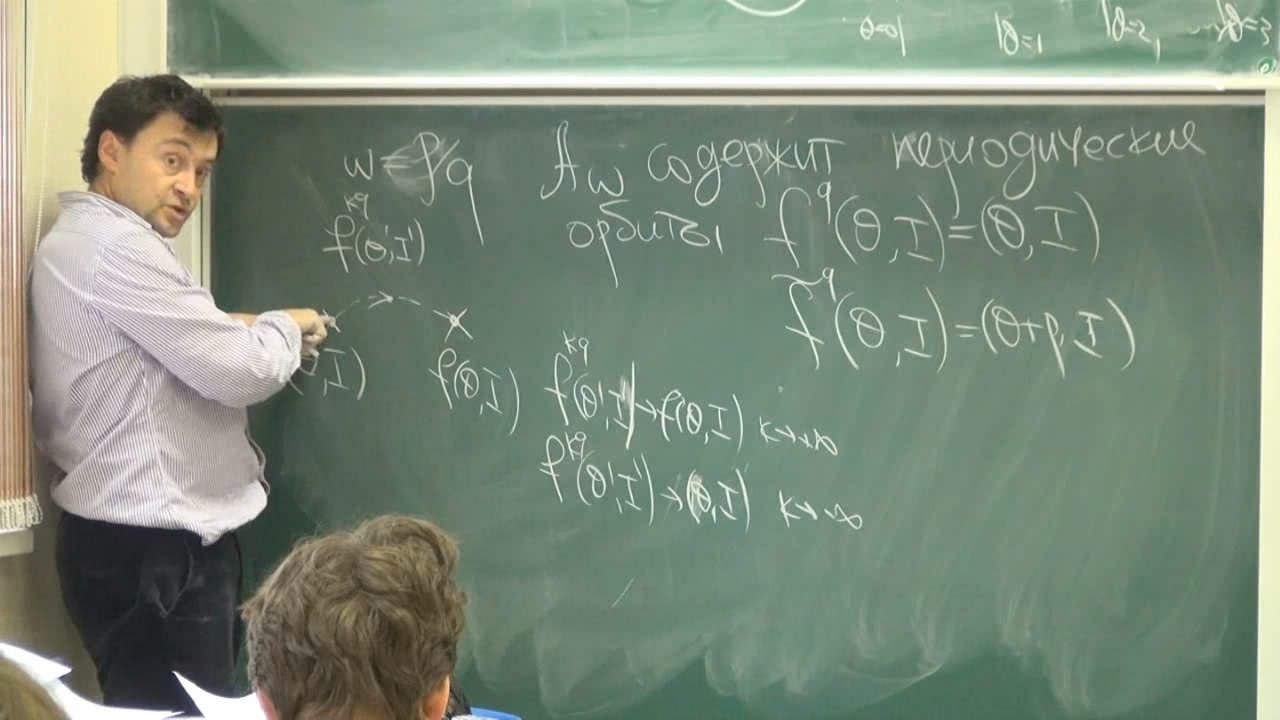
The famous ergodic hypothesis claims that a typical Hamiltonian dynamics on a typical energy surface is ergodic. However, KAM theory disproves this. It establishes a persistent set of positive measure of invariant KAM tori. The (weaker) quasi-ergodichypothesis, proposed by Ehrenfest and Birkhoff, says that a typical Hamiltonian dynamics on a typical energy surface has a dense orbit. This question is wide open. In early 60th Arnold constructed an example of instabilities for a nearly integrable Hamiltonian of dimension n>2 and conjectured that this is a generic phenomenon, nowadays, called Arnold diffusion. In the last two decades a variety of powerful techniques to attack this problem were developed. In particular, Mather discovered a large class of invariant sets and a developped delicate variational technique to shadow them. In two preprints: one joint with P. Bernard, K. Zhang and another with K. Zhang we prove Arnold's conjecture in dimension n=3.
План лекций МИНИКУРСА:
- Гипотезы о связи с диффузионными процессами.
- Cвязь со слабой КАМ-теорией и уравнения Гамильтона-Якоби.
- Нормальнo гиперболические инвариантные цилиндры и динамические аспекты.